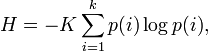|
Entropy and
Information / Entropía e Información Communication, Information and Coding Comunicación, Información y Codificación www.fgalindosoria.com/informatica/aspects/e_i/entropy_information/
Fernando Galindo Soria
English (www.fgalindosoria.com/en/ ) Español
(http://www.fgalindosoria.com/ ) Red de Desarrollo
Informático REDI Entropy and Information / Knowledge / Linguistic Aspects / Fractals and Chaos /.. Entropía e Información / Conocimiento / Aspectos Lingüísticos / Fractales y Caos, Datos;
Estructuras; Patrones; Normas; Dinero;
Código Genético, Sistema Nervioso, Neurotransmisores; Cuerdas, Ondas, Señales, Ruido,
Sonido, Música; Partículas; Mezclas, Soluciones, Compuestos; Campo, Espacio; Entidades, Atributos, Relaciones; Unidades de Materia, Energía e Información
(UMEI); Pensamiento; Noticias, Memes; Códices, Libros; Qbit, Entrelazamiento; Conjunto, Grupo, Anillo; Sistemas Conexionistas, Redes
Neurales; Sistemas Formales; Sistemas Evolutivos, Afectivos,
Concientes; Espacio de Caos, Espacio
Probabilístico, Espacio Métrico;
Estructuras Arborescentes, Dendritas;
Continuo, Discreto (Numerable, No Numerable) ; Multiarboles; Matrices;
recursividad;… Creación
de la página www Ciudad de México, 4
Abril del 2014
últimas actualizaciones 4 Abril del 2014 |
|
La entropía es una propiedad informática que mide el desorden de un sistema Fernando Galindo Soria 22 de Enero del 2011 Entropía, Principio de Incertidumbre, Energía del Vació, Onda Partícula
***************************************************************************** ***************************************************************************** Pioneros "The
formal study of information theory did not begin until 1924, when Harry
Nyquist, a researcher at Bell Laboratories, published a paper entitled “Certain
Factors Affecting Telegraph Speed.” Nyquist realized that communication
channels had maximum data transmission rates, and he derived a formula for
calculating these rates in finite bandwidth noiseless channels." Encyclopædia
Britannica http://global.britannica.com/EBchecked/topic/709313/Certain-Factors-Affecting-Telegraph-Speed Harry Nyquist trabajo teórico en la determinación de los requerimientos del ancho de banda para la transmisión de la información http://es.wikipedia.org/wiki/Harry_Nyquist “Certain factors affecting telegraph speed”,
Harry Nyquist, Bell System Technical
Journal, 3, 1924, pp 324-346. Certain Factors
Affecting Telegraph Speed H. Nyquist Bell System Technical
Journal, Volume 3, Issue 2, pages 324–346, April 1924 Presented at
the Midwinter Convention of the A. I. E. E., Philadelphia, Pa. February 4–8,
1924, and reprinted from the Journal of the A. I. E. E. Vol. 43, p. 124,
1924. "Synopsis:
This paper considers two fundamental factors entering into the maximum speed
of transmission of intelligence by telegraph. These factors are signal
shaping and choice of codes. The first is concerned with the best wave shape
to be impressed on the transmitting medium so as to permit of greater speed
without undue interference either in the circuit under consideration or in
those adjacent, while the latter deals with the choice of codes which will
permit of transmitting a maximum amount of intelligence with a given number
of signal elements. It is shown
that the wave shape depends somewhat on the type of circuit over which
intelligence is to be transmitted and that for most cases the optimum wave is
neither rectangular nor a half cycle sine wave as is frequently used but a
wave of special form produced by sending a simple rectangular wave through a
suitable network. The impedances usually associated with telegraph circuits
are such as to produce a fair degree of signal shaping when a rectangular
voltage wave is impressed. Consideration
of the choice of codes show that while it is desirable to use those involving
more than two current values, there are limitations which prevent a large
number of current values being used. A table of comparisons shows the relative
speed efficiencies of various codes proposed. It is shown that no advantages
result from the use of a sine wave for telegraph transmission as proposed by
Squier and others2 and that their arguments are based on erroneous
assumptions." http://onlinelibrary.wiley.com/doi/10.1002/j.1538-7305.1924.tb01361.x/abstract ***************************************************************************** Ralph Vinton Lyon Hartley "La noción de la información fue definida por primera vez por Ralph Vinton Lyon Hartley en 1927 como la cantidad de elecciones o respuestas "Sí" o "No", que permiten reconocer unívocamente un elemento cualquiera en un conjunto de ellos" http://www.tecnotopia.com.mx/informatica.htm
Ralph Vinton Lyon Hartley "IRE Medal of Honor, 1946, for his oscillator
and information proportionality law. This was an award from the Institute of Radio Engineers which
later merged into the Institute of
Electrical and Electronics Engineers; the award became the IEEE Medal of Honor." http://en.wikipedia.org/wiki/Ralph_Hartley "La medida de la información contenida en un evento se introdujo por Hartley en 1927. l definió la información (a veces denominado información propia) contenido en el evento X = i como: I {X = i} = logD ( 1/P {X = i}) = −logD P {X = i}" www.virtual.unal.edu.co/cursos/sedes/manizales/4040051/html/capitulos/cap_i/medida_y_fuentes.pdf
"Transmission of Information",
Ralph Vinton Lyon Hartley, Bell
System Technical Journal, July 1928, pp.535–563. Transmission
of Information Hartley,
R. V. L., Bell System Technical Journal 7: 3. July 1928 " Synopsis:
A quantitative measure of “information” is developed which is based on
physical as contrasted with psychological considerations. How the rate of
transmission of this information over a system is limited by the distortion
resulting from storage of energy is discussed from the transient viewpoint.
The relation between the transient and steady state viewpoints is reviewed.
It is shown that when the storage of energy is used to restrict the steady
state transmission to a limited range of frequencies the amount of
information that can be transmitted is proportional to the product of the
width of the frequency-range by the time it is available. Several
illustrations of the application of this principle to practical systems are
included. In the case of picture transmission and television the spacial
variation of intensity is analyzed by a steady state method analogous to that
commonly used for variations with time. " http://www3.alcatel-lucent.com/bstj/vol07-1928/articles/bstj7-3-535.pdf ***************************************************************************** Claude Elwood Shannon http://es.wikipedia.org/wiki/Claude_E._Shannon Information theory http://en.wikipedia.org/wiki/Information_theory Teoría de la información http://es.wikipedia.org/wiki/Teor%C3%ADa_de_la_informaci%C3%B3n Information entropy http://en.wikipedia.org/wiki/Information_entropy Entropía (información) Incluye Relación de la entropía
con la Teoría de la información http://es.wikipedia.org/wiki/Entrop%C3%ADa_%28informaci%C3%B3n%29
Information theory Wikipedia
20140314 "An analog
to thermodynamic entropy is information entropy. In 1948, while
working at Bell Telephone Laboratories electrical
engineer Claude Shannon set out to mathematically quantify
the statistical nature of "lost information" in phone-line signals.
To do this, Shannon developed the very general concept of information entropy, a fundamental
cornerstone of information theory. Although the story varies,
initially it seems that Shannon was not particularly aware of the close
similarity between his new quantity and earlier work in thermodynamics. In
1949, however, when Shannon had been working on his equations for some time,
he happened to visit the mathematician John
von Neumann. During their discussions, regarding what Shannon should call
the "measure of uncertainty" or attenuation in phone-line signals
with reference to his new information theory, according to one source:[10] "My greatest concern was what to call it. I thought of calling it
‘information’, but the word was overly used, so I decided to call it
‘uncertainty’. When I discussed it with John von Neumann, he had a better idea.
Von Neumann told me, ‘You should call it entropy, for two reasons. In the
first place your uncertainty function has been used in statistical mechanics
under that name, so it already has a name. In the second place, and more
important, nobody knows what entropy really is, so in a debate you will
always have the advantage" According to
another source, when von Neumann asked him how he was getting on with his
information theory, Shannon replied:[11] "The theory was in excellent shape, except that he needed a good
name for "missing information". "Why don’t you call it
entropy", von Neumann suggested. "In the first place, a
mathematical development very much like yours already exists in Boltzmann's
statistical mechanics, and in the second place, no one understands entropy
very well, so in any discussion you will be in a position of advantage." In 1948 Shannon
published his famous paper A Mathematical Theory of Communication, in
which he devoted a section to what he calls Choice, Uncertainty, and Entropy.[12]
In this section, Shannon introduces an H function of the following
form:
where K
is a positive constant. Shannon then states that "any quantity of this
form, where K merely amounts to a choice of a unit of measurement,
plays a central role in information theory as measures of information,
choice, and uncertainty." Then, as an example of how this expression
applies in a number of different fields, he references R.C. Tolman's 1938 Principles
of Statistical Mechanics, stating that "the form of H will be
recognized as that of entropy as defined in certain formulations of
statistical mechanics where pi is the probability of a
system being in cell i of its phase space… H is then, for
example, the H in Boltzmann's famous H theorem."
As such, over the last fifty years, ever since this statement was made,
people have been overlapping the two concepts or even stating that they are
exactly the same. Shannon's
information entropy is a much more general concept than statistical
thermodynamic entropy. Information entropy is present whenever there are
unknown quantities that can be described only by a probability distribution.
In a series of papers by E. T. Jaynes starting in 1957,[13][14]
the statistical thermodynamic entropy can be seen as just a particular
application of Shannon's information entropy to the probabilities of
particular microstates of a system occurring in order to produce a particular
macrostate." http://en.wikipedia.org/wiki/History_of_entropy
- Information_theory Reprinted with
corrections from The Bell System Technical Journal, Vol. 27, pp.
379–423, 623–656, July, October, 1948. A
Mathematical Theory of Communication By C. E.
SHANNON "INTRODUCTION THe
recent development of various methods of modulation such as PCM and PPM which
exchange bandwidth for signal-to-noise ratio has intensified the interest in
a general theory of communication. A basis for such a theory is contained in
the important papers of Nyquist1 and Hartley2 on this
subject. In the present paper we will extend the theory to include a number
of new factors, in particular the effect of noise in the channel, and the
savings possible due to the statistical structure of the original message and
due to the nature of the final destination of the information. The
fundamental problem of communication is that of reproducing at one point
either exactly or approximately a message selected at another point.
Frequently the messages have meaning; that is they refer to or are correlated
according to some system with certain physical or conceptual entities. These
semantic aspects of communication are irrelevant to the engineering problem.
The significant aspect is that the actual message is one selected from a set
of possible messages. The system must be designed to operate for each
possible selection, not just the one which will actually be chosen since this
is unknown at the time of design. If the
number of messages in the set is finite then this number or any monotonic
function of this number can be regarded as a measure of the information
produced when one message is chosen from the set, all choices being equally
likely. As was pointed out by Hartley the most natural choice is the
logarithmic function. Although this definition must be generalized
considerably when we consider the influence of the statistics of the message
and when we have a continuous range of messages, we will in all cases use an
essentially logarithmic measure. The logarithmic measure is more convenient
for various reasons: 1. It is practically more useful. Parameters
of engineering importance such as time, bandwidth, number of relays, etc.,
tend to vary linearly with the logarithm of the number of possibilities. For
example, adding one relay to a group doubles the number of possible states of
the relays. It adds 1 to the base 2 logarithm of this number. Doubling the
time roughly squares the number of possible messages, or doubles the
logarithm, etc. 2. It is nearer to our intuitive feeling as
to the proper measure. This is closely related to (1) since we intuitively
measures entities by linear comparison with common standards. One feels, for
example, that two punched cards should have twice the capacity of one for
information storage, and two identical channels twice the capacity of one for
transmitting information. 3. It is mathematically more suitable. Many
of the limiting operations are simple in terms of the logarithm but would
require clumsy restatement in terms of the number of possibilities. The
choice of a logarithmic base corresponds to the choice of a unit for
measuring information. If the base 2 is used the resulting units may be
called binary digits, or more briefly bits, a word suggested by J. W. Tukey.
A device with two stable positions, such as a relay or a flip-flop circuit,
can store one bit of information. N such devices can store N bits, since the
total number of possible states is 2N and log2 2N
=N. If the
base 10 is used the units may be called decimal digits. Since log2M = log10M / log10
2 = 3:32log10M; a decimal
digit is about 3 1/3 bits. A digit wheel on a desk computing machine has ten stable
positions and therefore has a storage capacity of one decimal digit. In
analytical work where integration and differentiation are involved the base e
is sometimes useful. The resulting units of information will be called
natural units. Change
from the base a to base b merely requires multiplication by logb
a. 1Nyquist, H., “Certain Factors Affecting Telegraph Speed,” Bell
System Technical Journal, April 1924, p. 324; “Certain Topics in
Telegraph Transmission Theory,” A.I.E.E. Trans., v. 47, April 1928, p.
617. 2Hartley, R. V. L., “Transmission of Information,” Bell System
Technical Journal, July 1928, p. 535." http://cm.bell-labs.com/cm/ms/what/shannonday/shannon1948.pdf "A Mathematical
Theory of Communication by Claude E. Shannon
A Note on the Edition Claude
Shannon's ``A mathematical theory of communication'' was first published in
two parts in the July and October 1948 editions of the Bell System Technical
Journal [1]. The paper has appeared in a number of republications
since:
The text
we present here is based on the BSTJ version with a number of
corrections. (The version on this site before May 18th 1998 was based on the University of Illinois Press version.) Here you
can find a PostScript (460 Kbytes), gzipped PostScript (146 Kbytes) and pdf (358 Kbytes) version of Shannon's paper. PDF
files can be viewed by Adobe's acrobat reader. Tarred and gzipped contents of
the directory (63 Kbytes) that contain the
LaTeX code for the paper is also available." http://cm.bell-labs.com/cm/ms/what/shannonday/paper.html ***************************************************************************** Recent
Contributions to The Mathematical Theory of Communication Warren
Weaver September,
1949 "Abstract This paper
is written in three main sections. In the first and third, W. W. is
responsible both for the ideas and the form. The middle section, namely “2)
Communication Problems at Level A” is an interpretation of mathematical
papers by Dr. Claude E. Shannon of the Bell Telephone Laboratories. Dr.
Shannon’s work roots back, as von Neumann has pointed out, to Boltzmann’s
observation, in some of his work on statistical physics (1894), that entropy
is related to “missing information,” inasmuch as it is related to the number
of alternatives which remain possible to a physical system after all the
macroscopically observable information concerning it has been recorded. L.
Szilard (Zsch. f. Phys. Vol. 53, 1925) extended this idea to a general
discussion of information in physics, and von Neumann (Math. Foundation of
Quantum Mechanics, Berlin, 1932, Chap. V) treated information in quantum
mechanics and particle physics. Dr. Shannon’s work connects more directly
with certain ideas developed some twenty years ago by H. Nyquist and R. V. L.
Hartley, both of the Bell Laboratories; and Dr. Shannon has himself
emphasized that communication theory owes a great debt to Professor Norbert
Wiener for much of its basic philosophy. Professor Wiener, on the other hand,
points out that Shannon’s early work on switching and mathematical logic
antedated his own interest in this field; and generously adds that Shannon
certainly deserves credit for independent development of such fundamental
aspects of the theory as the introduction of entropic ideas. Shannon has
naturally been specially concerned to push the applications to engineering
communication, whileWiener has been more concerned with biological
application (central nervous system phenomena, etc.). 1
Introductory Note on the General Setting of the Analytical Communication Studies 1.1
Communication 1.2 Three
Levels of Communications Problems Relative
to the broad subject of communication, there seem to be problems at three
levels. Thus it seems reasonable to ask, serially: LEVEL A.
How accurately can the symbols of communication be transmitted? (The
technical problem.) LEVEL B.
How precisely do the transmitted symbols convey the desired meaning? (The
semantic problem.) LEVEL C.
How effectively does the received meaning affect conduct in the desired way?
(The effectiveness problem.) 1.3
Comments 2
Communication Problems at Level A 2.1 A
Communication System and Its Problems 2.2
Information 2.3
Capacity of a Communication Channel 2.4
Coding 2.5 Noise 2.6
Continuous Messages 3 The
Interrelationship of the Three Levels of Communication Problems 3.1
Introductory 3.2
Generality of the Theory at Level A" The
Mathematical Theory of Communication Claude E
Shannon, Warren Weaver Univ of
Illinois Press, 1949 University
of Illinois Press Champaign, IL, USA, 1963 http://www.magmamater.cl/MatheComm.pdf Los trabajos de Nyquist, Hartley y aun los de Shannon y Weaver son trabajos que se desarrollaron a partir de problemas de ingeniería y sentaron las bases para el desarrollo de teorías que a su vez se han aplicado para resolver nuevamente problemas específicos, ya que son trabajos concretos desarrollados para resolver problemas concretos de manejo de señales. El comentario es porque mucha gente confunde el manejo de las matemáticas con el desarrollo de trabajos abstractos, sobre fundamentación o que no tienen que ver con los problemas reales, las matemáticas en este caso son herramientas básicas para resolver problemas de tecnoinformática (tecnologías de la información y comunicación), que a partir de esos trabajos se desarrollen y fundamenten las áreas es otra cosa.
***************************************************************************** Teoría de la Información y la Codificación Norman
Abramson Norman
Abramson From Wikipedia, the free encyclopedia "Norman
Manuel Abramson (April 1, 1932)[1]
is an American engineer and computer scientist, most known for developing the
ALOHAnet
system for wireless computer communication. ..... His early
research concerned radar signal characteristics and sampling
theory, as well as frequency modulation and digital communication channels, error correcting codes,[2]
pattern recognition and machine
learning and computing for seismic
analysis. In the late 1960s he worked on the ALOHAnet and
continued to develop spread spectrum techniques in the 1980s. http://en.wikipedia.org/wiki/Norman_Abramson Norman Abramson De Wikipedia, la enciclopedia libre "Norman Abramson (1 de abril de 1932) es un ingeniero informático estadounidense, conocido por ser el principal desarrollador de ALOHAnet. Comenzando la década de 1970, él y sus colaboradores pretendían conectar usuarios remotos con una computadora central situada en Honolulu. Hasta entonces la solución era conectar mediante cables submarinos, lo cual no parecía una solución muy satisfactoria. Gracias a él, se pudo transmitir datos por primera vez en una red inalámbrica." http://es.wikipedia.org/wiki/Norman_Abramson
Teoría de la Información y Codificación – Códigos
***************************************************************************** Entropía de Kolmogórov Hijos de la Entropia. 10 de septiembre de 2009 "La entropía de Kolmogórov se define como principio que mide la pérdida de información a lo largo de la evolución del sistema. Si por sistema entendemos que tenemos a nuestra sociedad actual, nos encontramos con un principio que absorbe una pérdida descomunal de información, siendo contradictorio por el absoluto dominio digital-global, ya que nos encontramos ante una continua desaceleración de vericidad en los dominios de la información, y eso produce la pérdida de información que mide el principio de la entropía de Kolmogórov. También es definida como la suma de exponentes de Liapunov(El Exponente Lyapunov o Exponente característico Lyapunov de un sistema dinámico es una cantidad que caracteriza el grado de separación de dos trayectorias infinitesimalmente cercanas)." http://hijosdelaentropia.blogspot.mx/2009/09/entropia-de-kolmogorov.html
19/09/2003 "Cuando Shannon publicó sus trabajos hacia 1.948, a los matemáticos en general les pareció algo excesivamente orientado a la tecnología como para tener interés en matemática pura. El gran Andrei Nikolaievich Kolmogorov fué la excepción, escribiendo en una ocasión: “La importancia del trabajo de Shannon para los matemáticos puros no fue totalmente apreciada desde el comienzo. Recuerdo cuando, en el Congreso Internacional de Matemáticos celebrado en Ámsterdam en 1.954, mis colegas norteamericanos, especialistas en probabilidades, creían que mi interés por los trabajos de Shannon eran algo exagerado ya que esto era más tecnología que matemática. Ahora, tales opiniones ni siquiera necesitan ser refutadas”
... Kolmogorov, .... Concretamente estableció la definición de entropía en el interior de un conjunto. Dado un conjunto, es necesario utilizar cierta cantidad de
información para delimitar sin ambigüedad cualquiera de sus subconjuntos
propios. Kolmogorov entendió que aquí era donde podía entrar el concepto de
entropía. Definió la entropía de un subconjunto en función del hecho
anterior, y la llamó e-entropía. (Léase
épsilon-entropía). Si C es un conjunto finito, podemos expresar por enumeración la lista de sus subconjuntos. A cada subconjunto le corresponderá simplemente su número de orden en la lista. El tamaño de la lista es de 2 elevado a N subconjuntos. Lo que expresado en sistema binario nos ocupa precisamente N bits. (Otra forma de verlo es teniendo en cuenta que podemos hacer corresponder un bit a cada posible elemento de los N en C , y para un subconjunto concreto, el j-ésimo bit vale 1 si está presente en el subconjunto, y 0 en caso contrario).
Kolmorogov definió la entropía de un subconjunto como
H(C)= log (N) donde el logaritmo está en base 2.
Para conjuntos no numerables su táctica fue el uso de e-recubrimientos de radio e (épsilon) arbitrario. La epsilon-entropía del subconjunto era al igual que en el caso numerable, el logaritmo en base 2 del número de elementos del e-recubrimiento mínimo para cubrir totalmente al conjunto. Un e-recubrimiento del conjunto C es un recubrimiento por conjuntos de diámetro menor o igual a 2e. En el caso se un segmento de recta, el número de elementos de un e-recubrimiento es precisamente (L/2e), de donde su e-entropía será:
H(C)=log (L/2e) , ....
De esta manera, Kolmogorov hecha un puente entre la teoría de la información y la abstracta teoría de conjuntos." http://tiopetrus.blogia.com/2003/091901-la-entropia-de-kolmogorov.php
***************************************************************************** ***************************************************************************** |
|
Ir a Portal de Fernando Galindo Soria Aspects of Information
/ Aspectos de la Información Datos; Entropía e
Información;
Conocimiento;
Estructuras; Patrones; Normas, dinero, neurotransmisores; ;
Cuerdas, ondas y partículas, señales, ruido; Mezclas, Soluciones, Compuestos; Aspectos
lingüísticos; Léxico, sintaxis, semántica;....Fractales y Caos;
Cristales; Campo, Espacio;....
Entidades, atributos, relaciones;.... Entropy and Information / Entropía e Información Entropy and Thermodynamics
/ Entropía y Termodinámica Entropy and
Information / Entropía e Información Maxwell's demon
/ El demonio de Maxwell Negentropy and Information
/ Neguentropía e Información negative entropy entropía negativa neg entropy neg entropía...... neguentropía negantropía sintropía ..... Current Research in
Entropy and Information Investigaciones Actuales sobre Entropía e Información |